Adopting Functional Perspectives

The greatest value of a picture is when it forces us to notice what we never expected to see.
(John W. Tukey)¹

The key riskyr data structure essentially describes a network of dependencies. This is best illustrated by the network diagram (see examples of plot_fnet() in the user guide and data formats). However, sometimes it is instructive to view all possible values of a parameter as a function of some other variable. A functional perspective illustrates how the value of some variable (or its values) changes as a function of another (and their values).

Functions

The basic format of a function is \(y = f(x)\), which illustrates how values of \(y\) depend on values of \(x\) given some function \(f\). riskyr provides two functions for viewing parameters as a function of other parameters (and their values).

Curves as a function of prevalence

The plot_curve() function draws the curves (or lines) of selected parameters as a function of the prevalence (with prev ranging from 0 to 1) for a given decision process or diagnostic test (i.e., given values of sens and spec):

\[y \ = \ f(\texttt{prev} \textrm{, from 0 to 1}) \textrm{ with } y \in \{\texttt{PPV}, \texttt{NPV}, \texttt{ppod}, \texttt{acc}\} \ \ \ \ \ \ (1)\]

As an example, reconsider our original scenario (on mammography screening, see user guide). Earlier, we computed a positive predictive value (PPV) of 7.8%. But rather than just computing a single value, we could ask: How do values of PPV develop as a function of prevalence? The plot_curve() function illustrates this relationship:

plot_curve(prev = .01, sens = .80, spec = (1 - .096), 
           what = c("prev", "PPV", "NPV"), 
           title_lbl = "Mammography screening", cex.lbl = .8)
#> Argument 'title_lbl' is deprecated. Please use 'main' instead.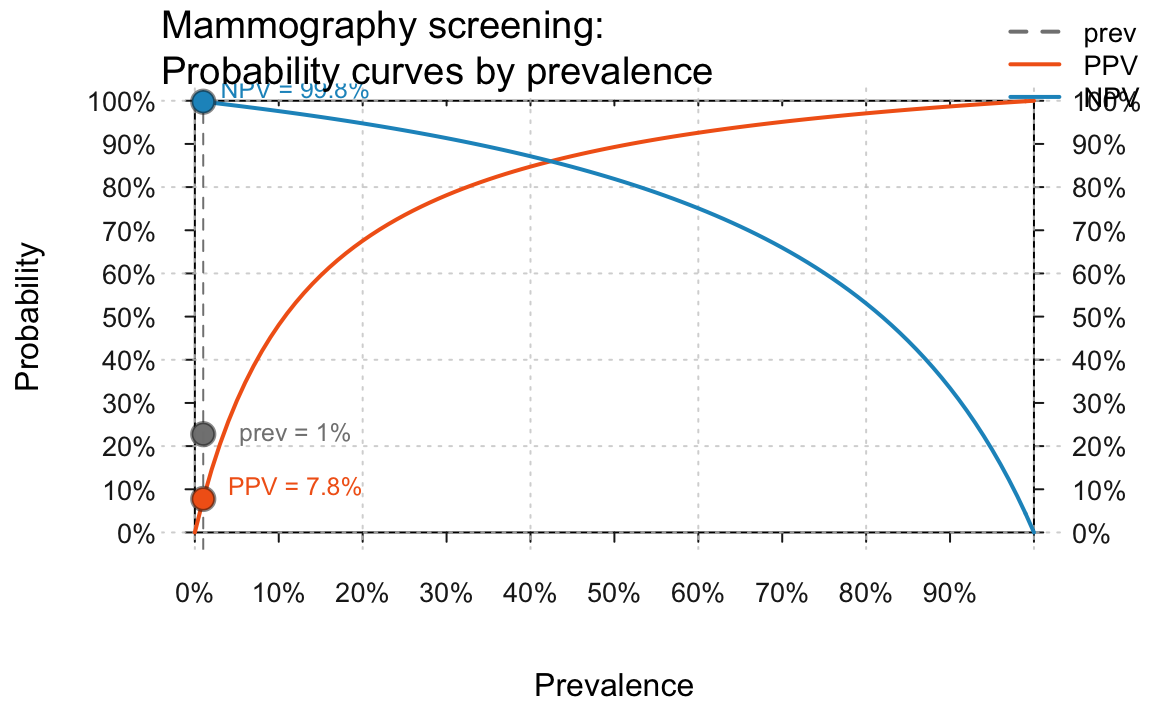

Showing PPV and NPV as a function of prevalence (for a prevalance of 1% and given values of sensitivity and specificity) in the original mammography screening scenario.

The curves illustrate that values of PPV and NPV crucially depend on the prevalence value prev in the current population. In fact, they actually vary across their entire range (i.e., from 0 to 1), rendering any communication of their value utterly meaningless without specifying the current population’s prevalence value.

The dependency of PPV and NPV on prev can be illustrated by assuming a higher prevalence rate. For instance, if we knew that some woman was genetically tested and known to exhibit the notorious BRCA1 mutation, the prevalence value of her corresponding population (given a positive mammography result in a routine screening) is increased to about 60% (graph not shown here to save space, but try running the following code for yourself):

high.prev <- .60   # assume increased prevalence due to BRCA1 mutation

plot_curve(prev = high.prev, sens = .80, spec = (1 - .096), 
           what = c("prev", "PPV", "NPV"), 
           title_lbl = "Mammography screening (BRCA1 mutation)", cex.lbl = .80)

This shows that — given an increased prevalence value prev of 60% — the positive predictive value PPV of a positive test result increases from 7.8% (in the standard population) to around 93% (given the BRCA1 mutation).

In addition, the actual values of population and test parameters are often unclear. The plot_curve() function reflects this by providing an uncertainty parameter uc that is expressed as a percentage of the specified value. For instance, the following assumes that our parameter values may deviate up to 5% from the specified values and marks the corresponding ranges of uncertainty as shaded areas around the curves that assume exact parameter values.

Both the notions of expressing probabilities as a function of prevalence and of uncertainty ranges for imprecise parameter estimates can be extended to other probabilities. The following curves show the full set of curves currently drawn by plot_curve(). In addition to the predictive values PPV and NPV, we see that the bias or proportion of positive decisions ppod and the overall accuracy acc also vary as a function of the prevalence prev:

high.prev <- .60   # assume increased prevalence due to BRCA1 mutation

plot_curve(prev = high.prev, sens = .80, spec = (1 - .096), 
           what = c("prev", "PPV", "NPV", "ppod", "acc"), 
           title_lbl = "Mammography screening (BRCA1 mutation)", uc = .05, cex.lbl = .80)
#> Argument 'title_lbl' is deprecated. Please use 'main' instead.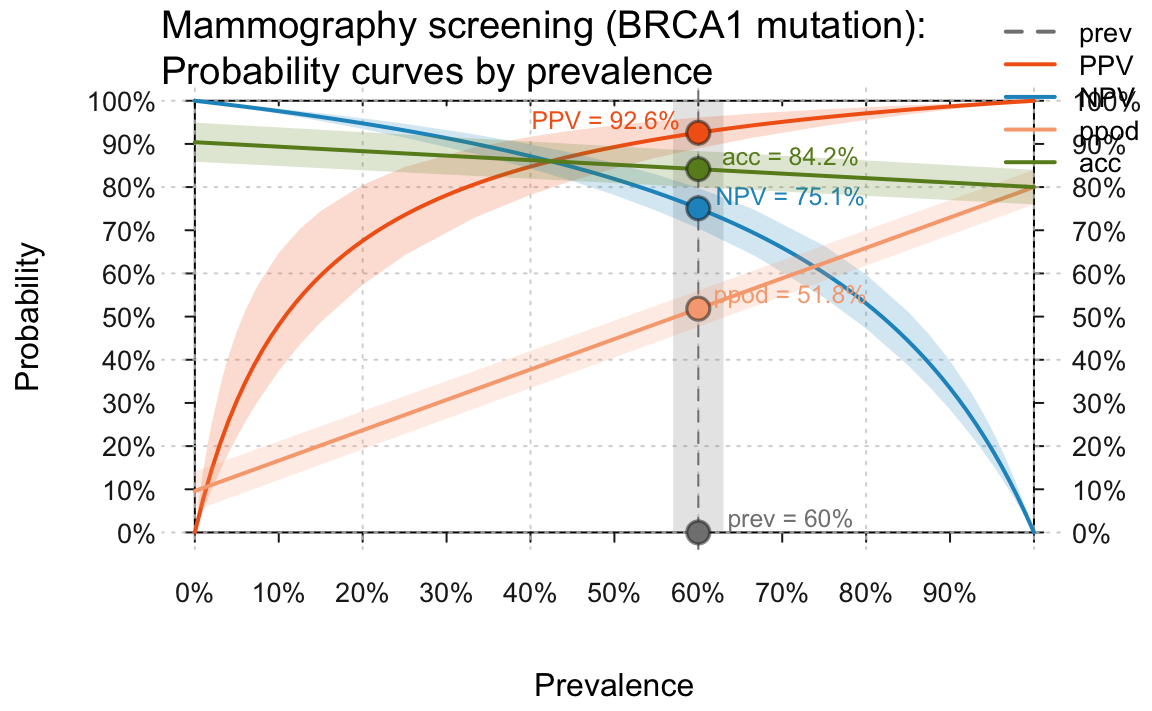

Curves that show PPV/NPV, ppod, and acc as a function of an prevalence (for given values of sensitivity and specificity) when assuming an increased prevalence of 60% and an uncertainty range of 5%.

Planes as a function of sensitivity and specificity (given a prevalence)

The plot_plane() function draws a plane for a selected parameter as a function of sensitivity and specificity values (with sens and spec both ranging from 0 to 1) for a given prevalence prev:

\[y \ = \ f(\texttt{sens} \times\ \texttt{spec} \textrm{, both from 0 to 1, for given value of } \texttt{prev}) \textrm{ with } y \in \{\texttt{PPV}, \texttt{NPV}, \texttt{ppod}, \texttt{acc}\} \ \ \ \ \ \ \ (2)\]

Some examples (not shown here, but please try evaluating the following function calls):

plot_plane(prev = high.prev, sens = .80, spec = (1 - .096), what = "PPV",  
           title_lbl = "A. Mammography (BRCA1)", cex.lbl = .8)
#> Argument 'title_lbl' is deprecated. Please use 'main' instead.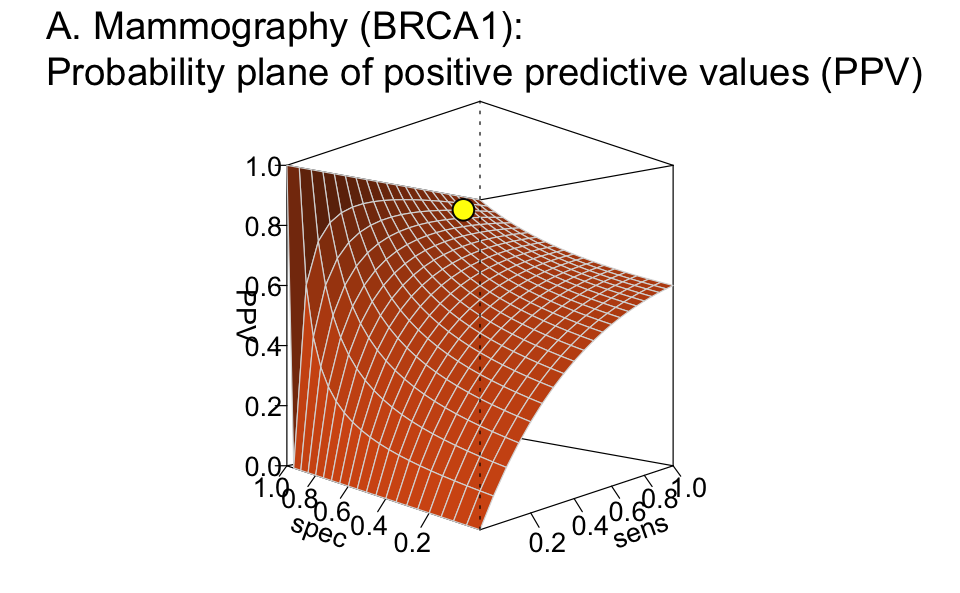

Plane showing the positive predictive value (PPV) as a function of sensitivity and specificity for a given prevalence.

Related plots (showing different probabilities) include:

plot_plane(prev = high.prev, sens = .80, spec = (1 - .096), what = "NPV",  
           title_lbl = "B. Mammography (BRCA1)", cex.lbl = .8)
plot_plane(prev = high.prev, sens = .80, spec = (1 - .096), what = "ppod", what_col = "firebrick", 
           title_lbl = "C. Mammography (BRCA1)", phi = 45, cex.lbl = .8)
plot_plane(prev = high.prev, sens = .80, spec = (1 - .096), what = "acc",  what_col = "forestgreen", 
           title_lbl = "D. Mammography (BRCA1)", cex.lbl = .8)

Overall, viewing conditional probabilities (like PPV or NPV, but also ppod or acc) as a function of other probabilities (e.g., prev, sens, spec or fart) often reveals unexpected relationships and can enable new insights.

Resources

The following resources and versions are currently available:

Type:	Version:	URL:
A. riskyr (R package):	Release version	https://CRAN.R-project.org/package=riskyr
	Development version	https://github.com/hneth/riskyr/
B. riskyrApp (R Shiny code):	Online version	https://riskyr.org/
	Development version	https://github.com/hneth/riskyrApp/
C. Online documentation:	Release version	https://hneth.github.io/riskyr/
	Development version	https://hneth.github.io/riskyr/dev/

Contact

We appreciate your feedback, comments, or questions.

Please report any riskyr-related issues at https://github.com/hneth/riskyr/issues/.
Contact us at contact.riskyr@gmail.com with any comments, questions, or suggestions.

All riskyr vignettes

Nr.	Vignette	Content
A.	User guide	Motivation and general instructions
B.	Data formats	Data formats: Frequencies and probabilities
C.	Confusion matrix	Confusion matrix and accuracy metrics
D.	Functional perspectives	Adopting functional perspectives
E.	Quick start primer	Quick start primer

Tukey, J.W. (1977), Exploratory data analysis. Reading, MA: Addison-Wesley. (p. vi).↩︎