Data Formats

Hansjörg Neth, SPDS, uni.kn

2021 03 31

The quest for certainty is the biggest obstacle to becoming risk savvy. (Gerd Gigerenzer)¹

A major challenge in mastering risk literacy is coping with inevitable uncertainty. Fortunately, uncertainty in the form of risk can be expressed in terms of probabilities and thus be measured and calculated or “reckoned” with (Gigerenzer, 2002). Nevertheless, probabilistic information is often difficult to understand, even for experts in risk management and statistics. A smart and effective way to communicate probabilities is by expressing them in terms of frequencies.

Two representational formats

The problems addressed by riskyr and the scientific discussion surrounding them can be framed in terms of two representational formats: Basically, risk-related information can be expressed in terms of frequencies or in terms of probabilities (see the user guide for background information.)

riskyr reflects this basic division by distinguishing between the same two data types and hence provides objects that contain frequencies (specifically, a list called freq) and objects that contain probabilities (a list called prob). But before we explain their contents, it is important to realize that any such separation is an abstract and artificial one. It may make sense to distinguish frequencies from probabilities for conceptual and educational reasons, but both in theory and in reality both representations are intimately intertwined.²

In the following, we first consider frequencies and probabilities by themselves, before showing how both are related. As a sneak preview, the following prism plot shows both frequencies (as nodes) and probabilities (as edges connecting the nodes) from two perspectives:

library("riskyr") # load the "riskyr" package

plot_prism(prev = .01, sens = .80, spec = NA, fart = .096,  # 3 essential probabilities
           N = 1000,       # 1 frequency
           area = "no",    # same size for all boxes
           p_lbl = "abb",  # show abbreviated names of probabilities on edges
           title_lbl = "Example")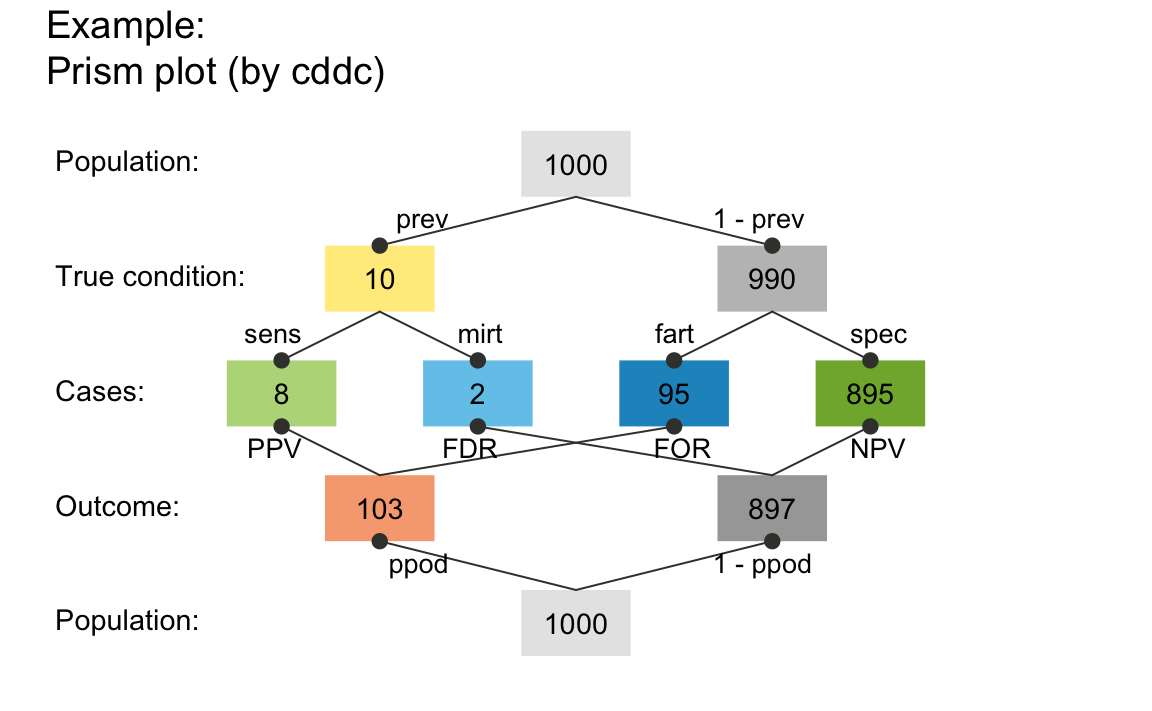

A prism plot showing frequencies as nodes and probabilities as edges linking nodes.

Frequencies

For our purposes, frequencies simply are numbers that can be counted — either 0 or positive integers.³

Definitions

The following 11 frequencies are distinguished by riskyr and contained in freq:

Nr.	Variable	Definition
1.	N	The number of cases (or individuals) in the population.
2.	cond_true	The number of cases for which the condition is present (TRUE).
3.	cond_false	The number of cases for which the condition is absent (FALSE).
4.	dec_pos	The number of cases for which the decision is positive (TRUE).
5.	dec_neg	The number of cases for which the decision is negative (FALSE).
6.	dec_cor	The number of cases for which the decision is correct (correspondence between decision and condition).
7.	dec_err	The number of cases for which the decision is erroneous (lack of correspondence between decision and condition).
8.	hi	The number of hits or true positives: condition present (TRUE) & decision positive (TRUE).
9.	mi	The number of misses or false negatives: condition present (TRUE) & decision negative (FALSE).
10.	fa	The number of false alarms or false positives: condition absent (FALSE) & decision positive (TRUE).
11.	cr	The number of correct rejections or true negatives: condition absent (FALSE) & decision negative (FALSE).

Perspectives: Basic vs. combined frequencies

The frequencies contained in freq can be viewed (or parsed) from two perspectives:

1. Top-down: From the entire population to different parts or subgroups:
   Whereas N specifies the population size, the other 10 frequencies denote the number of individuals or cases in some subset. For instance, the frequency dec_pos denotes individuals for which the decision or diagnosis is positive. As this frequency is contained within the population, its numeric value must range from 0 to N.

2. Bottom-up: From the 4 essential subgroups to various combinations of them:
   As the 4 frequencies hi, mi, fa, and cr are not further split into subgroups, we can think of them as atomic elements or four essential frequencies. All other frequencies in freq are sums of various combinations of these four essential frequencies. This implies that the entire network of frequencies and probabilities (shown in the network diagram above) can be reconstructed from these four essential frequencies.

Relationships among frequencies

The following relationships hold among the 11 frequencies:

1. The population size N can be split into several subgroups by classifying individuals by 4 different criteria:

   1. by condition (cd);
   2. by decision (dc);
   3. by accuracy (ac) (i.e., the correspondence of decisions to conditions);
   4. by the combination of condition and decision (i.e., a joint category).

Depending on the criterion used, the following relationships hold:

\[ \begin{aligned} \texttt{N} &= \texttt{cond_true} + \texttt{cond_false} & \textrm{(a)}\\ &= \texttt{dec_pos} + \texttt{dec_neg} & \textrm{(b)}\\ &= \texttt{dec_cor} + \texttt{dec_err} & \textrm{(c)}\\ &= \texttt{hi} + \texttt{mi} + \texttt{fa} + \texttt{cr} & \textrm{(d)}\\ \end{aligned} \]

Similarly, each of the subsets resulting from using the splits by condition (cd), by decision (dc), or by accuracy (ac), can also be expressed as a sum of two of the four essential frequencies. This results in three different ways of grouping the four essential frequencies:

1. by condition (cd) (corresponding to the two columns of the confusion matrix):

\[ \begin{aligned} \texttt{N} \ &= \ \texttt{cond_true} & +\ \ \ \ \ &\texttt{cond_false} & \textrm{(a)} \\ \ &= \ (\texttt{hi} + \texttt{mi}) & +\ \ \ \ \ &(\texttt{fa} + \texttt{cr}) \\ \end{aligned} \]

2. by decision (dc) (corresponding to the two rows of the confusion matrix):

\[ \begin{aligned} \texttt{N} \ &= \ \texttt{dec_pos} & +\ \ \ \ \ &\texttt{dec_neg} & \ \ \ \ \ \textrm{(b)} \\ \ &= \ (\texttt{hi} + \texttt{fa}) & +\ \ \ \ \ &(\texttt{mi} + \texttt{cr}) \\ \end{aligned} \]

3. by accuracy (ac) (or the correspondence of decisions to conditions, corresponding to the two diagonals of the confusion matrix):

\[ \begin{aligned} \texttt{N} \ &= \ \texttt{dec_cor} & +\ \ \ \ \ &\texttt{dec_err} & \ \ \ \ \textrm{(c)} \\ \ &= \ (\texttt{hi} + \texttt{cr}) & +\ \ \ \ \ &(\texttt{mi} + \texttt{fa}) \\ \end{aligned} \]

It may be tempting to refer to instances of dec_cor and dec_err as “true decisions” and “false decisions”. However, these terms invite conceptual confusion, as “true decisions” actually include cond_false cases (TN or cr cases) and “false decisions” actually include cond_true cases (FN or mi cases).

Probabilities

The notions of probability is as elusive as ubiquitous (see Hájek, 2012, for a solid exposition of its different concepts and interpretations). For our present purposes, probabilities are simply numbers between 0 and 1. These numbers are defined to reflect particular quantities and can be expressed as percentages, as functions of and ratios between other numbers (frequencies or probabilities).

Definitions

riskyr distinguishes between 13 probabilities (see prob for current values):

Nr.	Variable	Name	Definition
1.	prev	prevalence	The probability of the condition being TRUE.
2.	sens	sensitivity	The conditional probability of a positive decision provided that the condition is TRUE.
3.	mirt	miss rate	The conditional probability of a negative decision provided that the condition is TRUE.
4.	spec	specificity	The conditional probability of a negative decision provided that the condition is FALSE.
5.	fart	false alarm rate	The conditional probability of a positive decision provided that the condition is FALSE.
6.	ppod	proportion of positive decisions	The proportion (baseline probability or rate) of the decision being positive (but not necessarily TRUE).
7.	PPV	positive predictive value	The conditional probability of the condition being TRUE provided that the decision is positive.
8.	FDR	false detection rate	The conditional probability of the condition being FALSE provided that the decision is positive.
9.	NPV	negative predictive value	The conditional probability of the condition being FALSE provided that the decision is negative.
10.	FOR	false omission rate	The conditional probability of the condition being TRUE provided that the decision is negative.
11.	acc	accuracy	The probability of a correct decision (i.e., correspondence of decisions to conditions).
12.	p_acc_hi	–	The conditional probability of the condition being TRUE provided that a decision or prediction is accurate.
13.	p_err_fa	–	The conditional probability of the condition being FALSE provided that a decision or prediction is inaccurate or erroneous.

Note that the prism diagram (plot_prism) shows a total of 18 probabilities: 3 perspectives (by = "cd", by = "dc", and by = "ac") and 6 edges denoting the (marginal and conditional) probabilities for each perspective. However, we currently do not explicitly identify all possible probabilities.⁴

Non-conditional vs. conditional probabilities

Note that a typical riskyr scenario contains several marginal or non-conditional probabilities:

• The prevalence prev (1.) only depends on features of the condition.
• The proportion of positive decisions ppod (or bias) (6.) only depends on features of the decision.
• The accuracy acc (11.) depends on prev and ppod, but unconditionally dissects a population into two groups (dec_cor vs. dec_err).

The other probabilities are conditional probabilities based on three perspectives:

1. by condition: conditional probabilities (2. to 5.) depend on the condition’s prev and features of the decision.
   
2. by decision: conditional probabilities (7. to 10.) depend on the decision’s ppod and features of the condition.
   
3. by accuracy: conditional probabilities based on accuracy acc are currently computed, but – in the absence of a commonly accepted term — named p_acc_hi and p_err_fa (12. and 13.).

Relationships among probabilities

The following relationships hold among the conditional probabilities:

• The sensitivity sens and miss rate mirt are complements:

\[ \texttt{sens} = 1 - \texttt{mirt} \] - The specificity spec and false alarm rate fart are complements:

\[ \texttt{spec} = 1 - \texttt{fart} \] - The positive predictive value PPV and false detection rate FDR are complements:

\[ \texttt{PPV} = 1 - \texttt{FDR} \] - The negative predictive value NPV and false omission rate FOR are complements:

\[ \texttt{NPV} = 1 - \texttt{FOR} \]

It is possible to adapt Bayes’ formula to define PPV and NPV in terms of prev, sens, and spec:

\[ \texttt{PPV} = \frac{\texttt{prev} \cdot \texttt{sens}}{\texttt{prev} \cdot \texttt{sens} + (1 - \texttt{prev}) \cdot (1 - \texttt{sens})}\\ \\ \\ \texttt{NPV} = \frac{(1 - \texttt{prev}) \cdot \texttt{spec}}{\texttt{prev} \cdot (1 - \texttt{sens}) + (1 - \texttt{prev}) \cdot \texttt{spec}} \]

Although this is how the functions comp_PPV and comp_NPV compute the desired conditional probability, it is difficult to remember and think in these terms. Instead, we recommend thinking about and defining all conditional probabilities in terms of frequencies and relations between frequencies (see Neth et al., 2021 for details).

Probabilities as ratios between frequencies

The easiest way to think about, define, and compute the probabilities (contained in prob) is in terms of frequencies (contained in freq):

Nr.	Variable	Name	Definition	as Frequencies
1.	prev	prevalence	The probability of the condition being TRUE.	prev = cond_true/N
2.	sens	sensitivity	The conditional probability of a positive decision provided that the condition is TRUE.	sens = hi/cond_true
3.	mirt	miss rate	The conditional probability of a negative decision provided that the condition is TRUE.	mirt = mi/cond_true
4.	spec	specificity	The conditional probability of a negative decision provided that the condition is FALSE.	spec = cr/cond_false
5.	fart	false alarm rate	The conditional probability of a positive decision provided that the condition is FALSE.	fart = fa/cond_false
6.	ppod	proportion of positive decisions	The proportion (baseline probability or rate) of the decision being positive (but not necessarily TRUE).	ppod = dec_pos/N
7.	PPV	positive predictive value	The conditional probability of the condition being TRUE provided that the decision is positive.	PPV = hi/dec_pos
8.	FDR	false detection rate	The conditional probability of the condition being FALSE provided that the decision is positive.	FDR = fa/dec_pos
9.	NPV	negative predictive value	The conditional probability of the condition being FALSE provided that the decision is negative.	NPV = cr/dec_neg
10.	FOR	false omission rate	The conditional probability of the condition being TRUE provided that the decision is negative.	FOR = mi/dec_neg
11.	acc	accuracy	The probability of a correct decision (i.e., correspondence of decisions to conditions).	acc = dec_cor/N
12.	p_acc_hi	–	The conditional probability of the condition being TRUE provided that a decision or prediction is accurate.	p_acc_hi = hi/dec_cor
13.	p_err_fa	–	The conditional probability of the condition being FALSE provided that a decision or prediction is inaccurate or erroneous.	p_err_fa = fa/dec_err

Note that the ratios between frequencies are straightforward consequences of the probabilities’ definitions:

1. The unconditional probabilities (1., 6. and 11.) are proportions of the entire population:

   • prev = cond_true/N
   • ppod = dec_pos/N
   • acc = dec_cor/N

2. The conditional probabilities (2.–5., 7.–10., and 11.–12.) can be computed as a proportion of the reference group on which they are conditional. More specifically, if we schematically read each definition as “The conditional probability of \(X\) provided that \(Y\)”, then the ratio of the corresponding frequencies is X & Y/Y. More explicitly,

• the ratio’s numerator is the frequency of the joint occurrence (i.e., both X & Y) being the case;
• the ratio’s denominator is the frequency of the condition (Y) being the case.

When computing probabilities from rounded frequencies, their numeric values may deviate from the true underlying probabilities, particularly for small population sizes N. (Use the scale argument of many riskyr plotting functions to control whether probabilities are based on frequencies.)

Practice

An example

The following prism (or network) diagram is based on the following inputs:

• a condition’s prevalence of 50% (prev = .50);
• a decision’s sensitivity of 80% (sens = .80);
• a decision’s specificity of 60% (spec = .60);
• a population size of 10 individuals (N = 10);

and illustrates the relationship between frequencies and probabilities:

plot_prism(prev = .50, sens = .80, spec = .60,  # 3 essential probabilities
           N = 10,         # population frequency
           scale = "f",    # scale by frequency, rather than probability ("p") 
           area = "sq",    # boxes as squares, with sizes scaled by current scale  
           p_lbl = "num",  # show numeric probability values on edges
           title_lbl = "Probabilities as ratios between frequencies")
#> Argument 'title_lbl' is deprecated. Please use 'main' instead.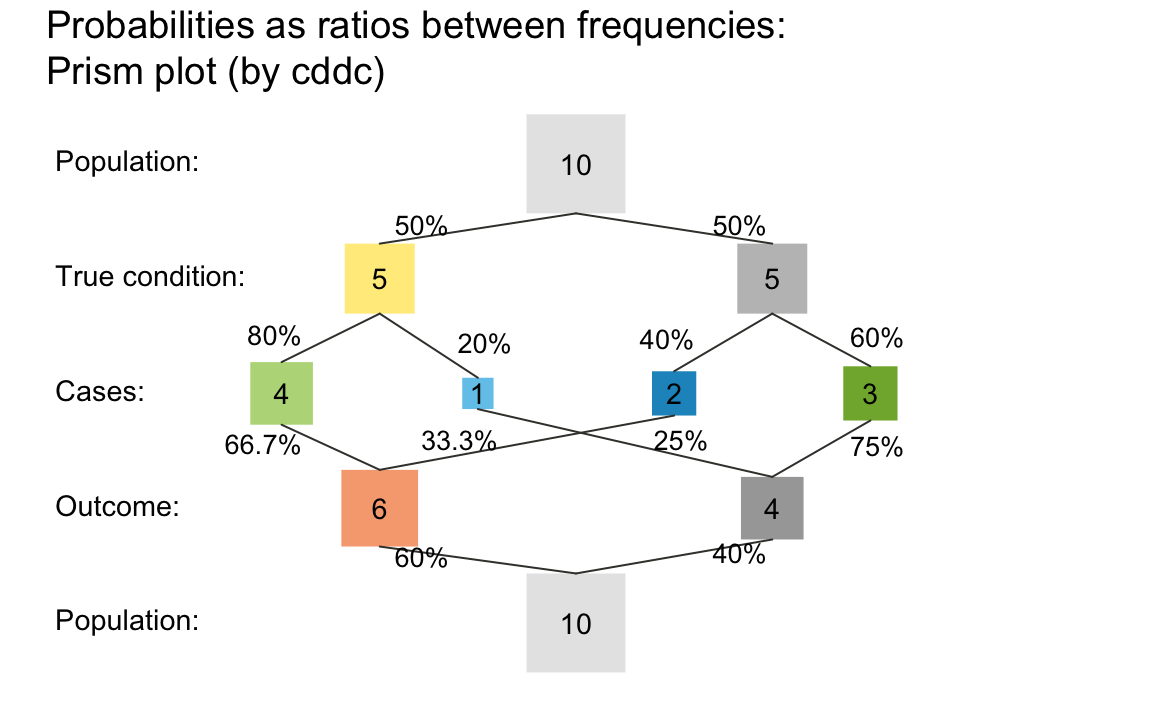

A prism plot showing how probabilities can be computed as ratios between frequencies.

Your tasks

1. Verify that the probabilities (shown as numeric values on the edges) match the ratios of the corresponding frequencies (shown in the boxes). What are the names of these probabilities?

2. What is the frequency of dec_cor and dec_err cases? Where do these cases appear in the diagram?

3. The parameter values in the example do not require any rounding of frequencies. Change them (e.g., to N = 5) and explore what happens when alternating between scale = "f" and scale = "p".

References

• Gigerenzer, G. (2002). Reckoning with risk: Learning to live with uncertainty. London, UK: Penguin.

• Gigerenzer, G. (2014). Risk savvy: How to make good decisions. New York, NY: Penguin.

• Gigerenzer, G., & Hoffrage, U. (1999). Overcoming difficulties in Bayesian reasoning: A reply to Lewis and Keren (1999) and Mellers and McGraw (1999). Psychological Review, 106, 425–430.

• Hájek, A (2012) Interpretations of Probability. In Edward N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy. URL: https://plato.stanford.edu/entries/probability-interpret/ 2012 Archive

• Hoffrage, U., Gigerenzer, G., Krauss, S., & Martignon, L. (2002). Representation facilitates reasoning: What natural frequencies are and what they are not. Cognition, 84, 343–352.

• Neth, H., Gradwohl, N., Streeb, D., Keim, D.A., & Gaissmaier, W. (2021). Perspectives on the 2x2 matrix: Solving semantically distinct problems based on a shared structure of binary contingencies. Frontiers in Psychology: Cognition, 11, 567817. doi: 10.3389/fpsyg.2020.567817 (Available online)

• Trevethan, R. (2017). Sensitivity, specificity, and predictive values: Foundations, pliabilities, and pitfalls in research and practice. Frontiers in Public Health, 5, 307. (Available online)

Resources

The following resources and versions are currently available:

Type:	Version:	URL:
A. riskyr (R package):	Release version	https://CRAN.R-project.org/package=riskyr
	Development version	https://github.com/hneth/riskyr/
B. riskyrApp (R Shiny code):	Online version	https://riskyr.org/
	Development version	https://github.com/hneth/riskyrApp/
C. Online documentation:	Release version	https://hneth.github.io/riskyr/
	Development version	https://hneth.github.io/riskyr/dev/

Contact

We appreciate your feedback, comments, or questions.

• Please report any riskyr-related issues at https://github.com/hneth/riskyr/issues/.

• Contact us at contact.riskyr@gmail.com with any comments, questions, or suggestions.

All riskyr vignettes

Nr.	Vignette	Content
A.	User guide	Motivation and general instructions
B.	Data formats	Data formats: Frequencies and probabilities
C.	Confusion matrix	Confusion matrix and accuracy metrics
D.	Functional perspectives	Adopting functional perspectives
E.	Quick start primer	Quick start primer

---

1. Gigerenzer, G. (2014). Risk savvy: How to make good decisions. New York, NY: Penguin. (p. 21).↩︎

2. For instance, we can distinguish between various types of probabilities (e.g., joint, marginal, and conditional probabilities) and natural frequencies provide a relational concept for expressing probabilities. See Neth et al., 2021 for details.↩︎

3. It seems plausible that the notion of a frequency is simpler than the notion of probability. Nevertheless, confusion is possible and typically causes serious scientific disputes. See Gigerenzer & Hoffrage, 1999, and Hoffrage et al., 2002, for different types of frequencies and the notion of natural frequencies.↩︎

4. For instance, some probabilities are the complements of others and do not have explicit names. Also, joint probabilities (e.g., the probabilities of hi, mi, fa, and cr) are not included in prob, but generated when needed (e.g., see plot_fnet()).↩︎